UUID というのは、全世界・全時間において一意性を持った識別子とされています。RFC 4122 の言葉を借りると、
A UUID is 128 bits long, and can guarantee uniqueness across space and time
とされています。
ですが、128 bit という有限長なんだから 回試行すれば少なくとも 1 回は生成した UUID が衝突するということになります。UUID は万能じゃねーんだ。冷静になれ。
UUID ってのは一意性が「保証」されているわけじゃなく、「実用上は一意と見做せる」ということになります。ですから、衝突する確率というのは 0 にはなりません。じゃぁ、果たしてどのくらいの確率で衝突が発生するのか、計算してみましょう。
計算のまえに結論を言う。回 UUID を生成したときに衝突が発生する確率は
くらい。
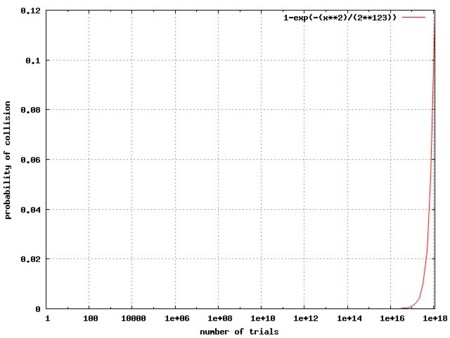
試行回数に対する衝突確率の伸びをグラフ化するとこんなかんじ。
軸はログスケールな。
前提
確率的に計算できそうなの UUID の Version 4 しかなさそうです。Version 4 では、128 bit のうち、122 bit にランダムな数値をセットして UUID とします (残りの 6 bit は固定値です)。
定式化
ここでは、「version 4 の方法で 回 UUID を生成したとき、それらが 1 つでも衝突してしまう確率
」を求めます。
"1 つでも"というところからピンと来ると思いますが、これは "衝突が一切発生しない" という事象に対する背反事象になります。このため、まずは衝突が一切発生しない確率をもとめ、それを 1 から引くという考え方をするのが王道です。
計算
順を追って考えましょう。
回の試行のうちの、最初の 1 回目を考えます。このとき、衝突する UUID は存在しないので、衝突しない確率は 1 (100 %) です。
回の試行のうちの、2 回目を考えます。このとき、1 回目に生成した UUID と衝突する可能性があります。UUID として発生し得るパターンは
パターンあるので、衝突する確率は
になり、衝突しない確率は
になります。
回の試行のうちの、3 回目を考えます。このとき、1 回目に生成した UUID、あるいは 2 回目に生成した UUID と衝突する可能性があります。したがって、衝突する確率は
になり、衝突しない確率は
になります。
- ...
回の試行のうちの、n 回目を考えます。このとき、1 回目から
回目に生成した UUID と衝突する可能性があります。したがって、衝突する確率は
になり、衝突しない確率は
になります。
以上から、n 回の試行において衝突が一切発生しない確率は、
ということになります。
従って、衝突が発生する確率 は、
です。
近似しましょう
で、こんな式を見せられても、実値を計算するのがマジでダルいですから、近似しましょう。というのを何とかして綺麗にしてやりたい。
ここで、指数関数のテイラー展開を思い出すと、
のとき、
です。試行回数
が
となる範囲を考えることにすると、
この指数関数のテイラー展開を利用して、
と近似できます。
これを の式に代入し、おなじみの公式
を使うと、
が導けます。
とすれば、
になります。かなりきれいになりました。
じゃぁ衝突確率が  になるときの試行回数
になるときの試行回数  はどのくらいなの
はどのくらいなの
衝突が発生する確率 が
になるための試行回数
を求めてみましょう。
を
に対して解けば良いです。
これ、わりとかんたんで、
になります。
これをグラフにしてみると以下のようなかんじになります。
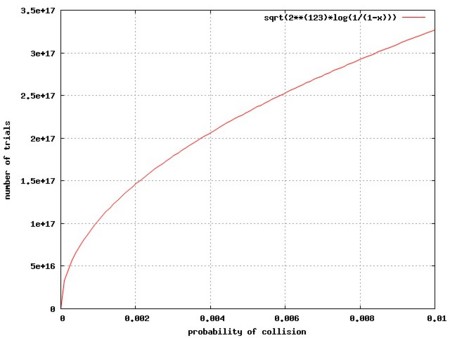
たとえば、衝突確率が 1 % () とすると、必要な試行回数は
回くらいですね。