ルベーグの単調収束定理は次のようなもので、非負値可測関数列$\lbrace f _{n} \rbrace$が単調増加列であることを必要としています。
$E$の上で$0 \leq f _{1} \leq f _{2} \leq \cdots \leq f _{n} \cdots, \displaystyle \lim _{n \to \infty} f _{n} = f$ならば、$\displaystyle \lim _{n \to \infty} \int _{E} f _{n} d\mu = \int _{E} f d\mu$が成り立つ。
では単調増加列ではない非負値可測関数列に対してどのような性質が成立するのか。それを1つ示したものがファトゥの補題です。
ファトゥの補題
ファトゥの補題は、次のように表されます。
$E$の上で$f _{n} \geq 0$ならば以下が成り立つ。
$$ \int _{E} \varliminf _{n \to \infty} f _{n} d\mu \leq \varliminf _{n \to \infty} \int _{E} f _{n} d\mu $$
ここでいくつか見慣れない操作$\displaystyle \varliminf _{n \to \infty}$がでてきているので、まずはそれについて記述します。
関数列の下極限・上極限
集合$E$上の関数列$\lbrace f _{n} \rbrace$に対して、
$$ \left( \varliminf _{n \to \infty} f _{n} \right) (x) := \lim _{n \to \infty} \left( \inf _{k \geq n} f _{k} (x) \right) $$
として定義される$E$上の関数$\displaystyle \varliminf _{n \to \infty} f _{n}$を関数列$\lbrace f _{n} \rbrace$の下極限といいます。
下極限があるなら当然上極限もあり、次のように定義されます。
$$ \left( \varlimsup _{n \to \infty} f _{n} \right) (x) := \lim _{n \to \infty} \left( \sup _{k \geq n} f _{k} (x) \right) $$
定義から明らかに $\displaystyle \varliminf _{n \to \infty} f _{n} \leq \varlimsup _{n \to \infty} f _{n}$ が成り立ちます。
また、$\displaystyle \varliminf _{n \to \infty} f _{n} = \varlimsup _{n \to \infty} f _{n}$ が成り立つとき、極限$\displaystyle \lim _{n \to \infty} f _{n}$が存在し、$\displaystyle \lim _{n \to \infty} f _{n} = \varliminf _{n \to \infty} f _{n} = \varlimsup _{n \to \infty} f _{n}$ となります。
ファトゥの補題の証明
ファトゥの補題は、ルベーグの単調収束定理を利用して証明できます。
まず、$g _{n}(x) = \displaystyle \inf _{k \geq n} f _{k} (x)$とおくと$g _{n} \geq 0$であり、関数列の下極限の定義から$\lbrace g _{n} \rbrace$は単調増加列であることが分かります。 また、$E$の各点で$\displaystyle \lim _{n \to \infty} g _{n} (x) = \varliminf _{n \to \infty} f _{n} (x)$が成り立ちます。
このため$g _{n}$に対してルベーグの単調収束定理が適用でき、即座に次のことが言えます。
$$ \lim _{n \to \infty} \int _{E} g _{n} d\mu = \int _{E} \varliminf _{n \to \infty} f _{n} d\mu $$
一方、$g _{n} \leq f _{n}$であるため、$\displaystyle \int _{E} g _{n} d\mu \leq \int _{E} f _{n} d\mu$が成り立ちます。 上の式から$\displaystyle \int _{E} g _{n} d\mu$に$n \to \infty$のときの極限が存在することに注意して、この両辺の下極限を取ります。
$$ \begin{align} \lim _{n \to \infty} \int _{E} g _{n} d\mu &\leq \varliminf _{n \to \infty} \int _{E} f _{n} d\mu & (\because \varliminf _{n \to \infty} \int _{E} f _{n} d\mu = \varliminf _{n \to \infty} \int _{E} f _{k} d\mu) \ \end{align} $$
これら2つの式を合わせると、次のようにファトゥの補題が導かれます。
$$ \begin{align} \int _{E} \varliminf _{n \to \infty} f _{n} d\mu &\leq \varliminf _{n \to \infty} \int _{E} f _{n} d\mu \end{align} $$
ファトゥの補題で等号が成立しない例
ではファトゥの補題で等号が成立しない例を考えてみましょう。
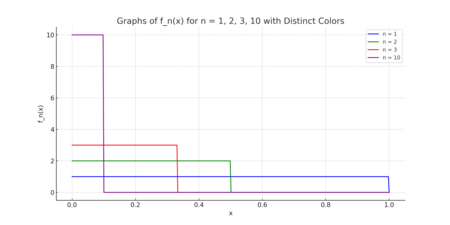
$E = [0, 1]$とし、$f _{n}$を次のように定義します。
$$ f _{n} (x) = \begin{cases} n & (0 \leq x < \frac{1}{n}) \newline 0 & (\frac{1}{n} \leq x \leq 1) \end{cases} $$
$n$をいくつかとってグラフ化するとこんな感じで、$\lbrace f _{n} \rbrace$は単調増加列ではありません。
まず$\displaystyle \int _{E} \varliminf _{n \to \infty} f _{n} d\mu$を計算します。下極限の定義から、$\displaystyle \varliminf _{n \to \infty} f _{n} (x) = 0$が成り立つのは自明でしょう。よって$\displaystyle \int _{E} \varliminf _{n \to \infty} f _{n} d\mu = 0$となります。
次に$\displaystyle \varliminf _{n \to \infty} \int _{E} f _{n} d\mu$を計算します。$f _{n}$の定義から、$\displaystyle \int _{E} f _{n} d\mu = 1$が成り立ちます。よって$\displaystyle \varliminf _{n \to \infty} \int _{E} f _{n} d\mu = 1$となります。
従って次のような不等式となり、等号は成立しません。
$$ \int _{E} \varliminf _{n \to \infty} f _{n} d\mu = 0 < 1 = \varliminf _{n \to \infty} \int _{E} f _{n} d\mu $$