以前、OpenTelemetry CollectorのLoad Balancing Exporterを使ってメトリクスを複数のWorkerに分散する仕組みを構築した記事を書きました。
あの構成では、Consistent Hash Ringを使って時系列ごとにWorkerへルーティングしています。Consistent Hashingの目的はノード数が増減してもキーの割り当て変動を最小限に抑えることですが、僕が想定しているWorker数は2台とか3台程度です。この程度の少数のノード数で、実際にどのくらいの影響が出るのか気になりました。
せっかくなので、今回はConsistent Hashingをモデル化して、ノード数が少ないときの影響を分析してみます。さらに、Load Balancing Exporterが内部で使っているVirtual Nodesという仕組みについても、その改善効果を見ていきます。
Consistent Hashingの基本的な仕組み
Consistent Hashingは、分散システムでキーを複数のノードに割り当てるアルゴリズムです。目的は、ノードが増減したときのキー移動を最小限に抑えること。これにより、キャッシュの無効化やステートの再構築を減らせます。
基本的なアイデアは、ハッシュ値の空間を円環(Hash Ring)として扱うことです。ノードとキーをそれぞれハッシュ化してRing上に配置し、キーは時計回りで最初に見つかるノード(これをsuccessor(後続ノード)と呼びます)に割り当てられます。
これを図で見てみましょう。
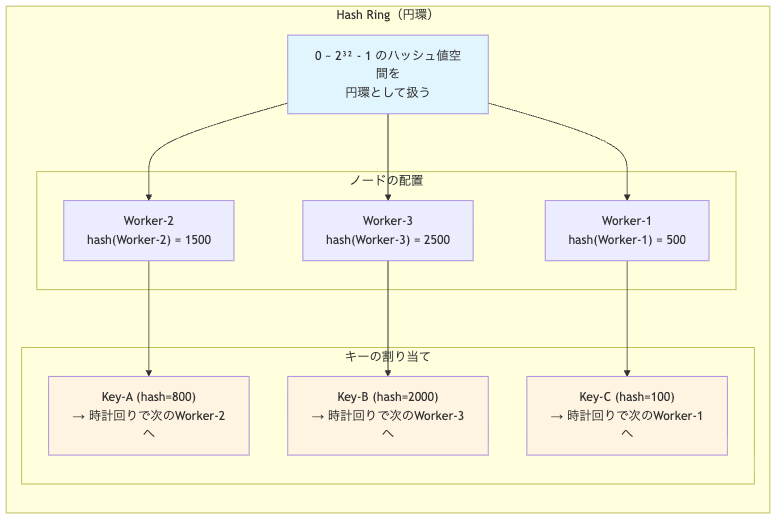
この方式の良さは、ノードを1台追加したときに移動するキーが、そのノードが新しく担当する区間のキーだけで済む点です。他のキーの割り当ては変わりません。
単純なモジュロ演算(node = hash(key) mod N)だと、Nが変わった瞬間にほぼ全てのキーの割り当て先が変わってしまいます。これと比べると、Consistent Hashingの局所性は圧倒的に優れています。
ノード数が少ないときの影響を数式で見てみる
では、ノード数Nが2台とか3台みたいに少ない場合、実際にどの程度の影響が出るんでしょうか。これを分析してみます。
キー移動率の定義と期待値
まず、「キー移動率」の定義をしておきます。$N$台のノードから$(N+1)$台にスケールアウトする場合、キー移動率とは、新しいノードに再割り当てされるキーの割合のことです。つまり、全キーのうち、従来とは異なるノードに移動するキーの比率を指します。
新しいノードを追加したとき、どのくらいのキーが移動するんでしょうか。
リング上に$N+1$個のノードが一様ランダムに配置されているとき、任意のキーから見て時計回りで最初に当たるノード(successor)がどれであるかは、対称性により等確率です。新ノードがsuccessorになる確率は次の通りです。
$$\Pr(\text{新ノードがsuccessor}) = \frac{1}{N+1}$$
期待されるキー移動率は次のようになります。
$$\mathbb{E}[\text{移動率}] = \frac{1}{N+1}$$
これを具体的な数値で見てみましょう。
| 既存ノード数N | 追加後 | 期待移動率 |
|---|---|---|
| 2 | 3 | 1/3 ≈ 33.3% |
| 3 | 4 | 1/4 = 25.0% |
| 4 | 5 | 1/5 = 20.0% |
| 9 | 10 | 1/10 = 10.0% |
N=2から3台に増やすと、約33%のキーが移動します。これは結構な割合です。DeltaToCumulativeみたいなステートフルな処理では、移動したキーに対応する状態のリセットが発生します。そのため、一時的にメトリクスの連続性を失う可能性があります。
ノード数が少ないと、スケールアウト時の影響は無視できないレベルになりますね。
負荷偏り:なぜDirichlet分布なのか
次に、各ノードの担当する負荷の偏りを見てみます。
N個のノードをRing上へ一様ランダムに配置すると、各ノードは一定の区間を担当します。リング全体を1とした場合、この区間の長さが各ノードの負荷割合を表します。これを担当率と呼びます。
この担当率は Dirichlet(1,1,...,1)分布 に従います。
「なんでDirichlet分布なの?」という点ですが、リング$[0,1)$上にN個のノードを一様ランダムに配置したとき、各ノードの担当率を $L_1, L_2, \dots, L_N$ とすると、以下の性質があります。
- 各担当率は非負:$L_i \ge 0$
- 合計が1(リング一周):$\sum_{i=1}^N L_i = 1$
- 全てのノードが対称(どのノードも同等に扱われる)
この3つの性質を満たす確率分布が、まさに Dirichlet(1,1,...,1)分布なんです。これは「単体上の一様分布」と呼ばれるもので、N個の成分が非負で合計が1になる確率ベクトルを生成します。
パラメータが全て1なので、どの区間も等しく扱われ、リング上での位置による偏りはありません。つまり、ランダムな配置から自然に生まれる偏りを表現しています。
Dirichlet分布から導かれる統計量
Dirichlet分布の数学的性質から、各ノードの担当率について以下が導出できます。
期待値: $$\mathbb{E}[L_i] = \frac{1}{N}$$
これは直感的で、各ノードが平均的には均等に担当することを意味します。
分散:
Dirichlet(1,1,...,1)分布の場合、一般式は $\mathrm{Var}(L_i) = \frac{\alpha_{i}(\alpha_{0} - \alpha_{i})}{\alpha_{0}^{2}(\alpha_{0}+1)}$ です。ここで $\alpha_{0} = \sum \alpha_{i}$ とします。この一般式に $\alpha_{i}=1$、$\alpha_{0}=N$ を代入すると、次のようになります。
$$\mathrm{Var}(L_i) = \frac{1 \cdot (N-1)}{N^{2}(N+1)} = \frac{N-1}{N^{2}(N+1)}$$
標準偏差は次のようになります。
$$\sigma = \sqrt{\frac{N-1}{N^{2}(N+1)}}$$
この式は、Nが十分大きいときに $\sigma \approx \frac{1}{N^{3/2}}$ と近似できますが、N=2や3のような小さい値では正確な式を使う必要があります。いずれにせよ、ノード数Nが少ないと標準偏差が大きくなり、負荷の偏りが大きくなります。
最大区間長:
ここで、最大区間長 $L_{\max}$ とは、N個のノードの中で最も多くの負荷を担当するノードの区間率のことです。つまり、次のようになります。
$$L_{\max} = \max_{i=1,\dots,N} L_i$$
この最大値がどの程度になるかですが、直感的には以下のように考えられます。
- 平均的な区間長は $1/N$
- しかし、たまたま隣接ノード間の距離が遠い場合、その区間は大きくなる
- N個の区間のうち最大のものは、平均の何倍くらいになるか
最大区間長の期待値の導出
最大値の期待値は、以下の積分公式で計算できます。
$$\mathbb{E}[L_{\max}] = \int_{0}^{1} P(L_{\max} > t) \, dt$$
ここで、$P(L_{\max} > t)$ は「最大区間が$t$以上になる確率」です。これは補集合を使って以下のように書き換えられます。
$$P(L_{\max} > t) = 1 - P(\text{すべての区間が} t \text{以下})$$
N個の区間がすべて$t$以下になる確率を求めるには、包除原理を使います。リング上にN個の点をランダム配置したとき、$k$個の区間がそれぞれ長さ$t$を超えると、それらの合計だけで $kt$ 以上の長さが必要です。リング全体の長さは1なので、$kt \leq 1$ でなければなりません。
包除原理により、次のようになります。
$$P(\text{すべて} \leq t) = \sum_{k=0}^{\lfloor 1/t \rfloor} (-1)^{k} \binom{N}{k} (1-kt)^{N}$$
この式の $(1-kt)^{N}$ 項は、「特定の$k$個の区間がそれぞれ長さ$t$を超える制約の下で、N個の点がリング上へ配置可能な確率」を表しています。$k$個の区間がそれぞれ最低でも長さ$t$を持つと、合計で $kt$ の長さが必要です。リング全体の長さが1なので、残りは $1-kt$ です。N個の点をこの残りの空間へランダムに配置する確率が $(1-kt)^{N}$ となります。
包除原理では、「特定の$k$個の区間が$t$を超える」という制約を持つケースを、二項係数 $\binom{N}{k}$ で数え上げ、交互に加減します。
- $k=0$の項:制約なし($\binom{N}{0} \times 1^{N} = 1$)
- $k=1$の項:特定の1つの区間が$t$を超える制約を持つN通りのケースを引く
- $k=2$の項:特定の2つの区間が$t$を超える制約を持つ $\binom{N}{2}$ 通りのケースを足す(重複を補正)
- $k≥3$の項:同様に交互に加減を繰り返す
結果として、「すべての区間が$t$以下」の確率が得られます。
これを積分すると次のようになります。
$$\mathbb{E}[L_{\max}] = \int_{0}^{1} \left[1 - \sum_{k=0}^{N-1} (-1)^{k} \binom{N}{k} (1-kt)^{N}\right] dt$$
この積分を項ごとに実行すると、各項が $1/k$ の形の係数を生み出します。計算の詳細は省略しますが、最終的に次のようになります。
$$\mathbb{E}[L_{\max}] = \frac{1}{N} \sum_{k=1}^{N} \frac{1}{k} = \frac{H_N}{N}$$
ここで $H_N = 1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{N}$ は第N調和数です。つまり、最大区間長の期待値は、平均 $1/N$ の $H_N$ 倍まで膨らみます。
具体的な数値例を見てみましょう。
| ノード数N | 期待担当率 | 標準偏差σ | 最大担当率(期待値) | 最大/平均 |
|---|---|---|---|---|
| 2 | 50.0% | 28.9% | 75.0% | 1.50倍 |
| 3 | 33.3% | 23.6% | 61.1% | 1.83倍 |
| 4 | 25.0% | 19.4% | 52.1% | 2.08倍 |
| 5 | 20.0% | 16.3% | 45.7% | 2.28倍 |
| 10 | 10.0% | 9.0% | 29.3% | 2.93倍 |
N=3のとき、期待担当率は33.3%ですが、標準偏差が23.6%もあります。最大担当率は約61%に達し、平均の1.8倍です。つまり、3台のWorkerがあっても、運が悪ければ1台だけが2倍近い負荷を受ける可能性があるわけです。
ノード数が少ないと、負荷の偏りも結構大きいんですね。
Virtual Nodesによる負荷偏り削減
この負荷偏りを改善する手法が Virtual Nodes(仮想ノード) です。実は、OpenTelemetry CollectorのLoad Balancing Exporterは、デフォルトで各Workerに対して100個の仮想ノードを使う実装になっています。
Virtual Nodesの仕組み
Virtual Nodesは、1台の物理ノードを複数の仮想的なノードとしてRing上に配置する手法です。例えば、3台の物理Workerがそれぞれ100個の仮想ノードを持つと、Ring上には合計300個の点が配置されます。
なぜDirichlet(V,V,...,V)分布になるのか
Virtual Nodesを使うと、各物理ノードの担当率は Dirichlet(V,V,...,V)分布 に従います。Vは仮想ノード数(この場合100)です。
これがなぜそうなるのか、ステップを追って説明します。
ステップ1:Ring上の仮想ノード配置
M台の物理ノードが各V個の仮想ノードを持つとき、Ring上には合計 $M \times V$ 個の仮想ノードが一様ランダムに配置されます。これにより、$M \times V$ 個の区間が生まれます。
各区間の長さを $l_1, l_2, \dots, l_{M \times V}$ とします。前のセクションで説明した理由により、これらは Dirichlet(1,1,...,1)分布($M \times V$ 次元)に従います。
ステップ2:物理ノードごとの集約
物理ノード $j$ の担当率 $S_j$ は、そのノードに属するV個の仮想ノードの区間長の合計です。
$$S_j = \sum_{k=1}^{V} l_{j,k}$$
ここで、$l_{j,1}, l_{j,2}, \dots, l_{j,V}$ は物理ノード $j$ に属するV個の区間長です。
ステップ3:Dirichlet分布の加法性
ここで重要なのが、Dirichlet分布の加法性という性質です。これは以下のような性質です。
$(X_1, X_2, \dots, X_n) \sim \mathrm{Dirichlet}(\alpha_1, \alpha_2, \dots, \alpha_n)$ のとき、成分をグループ化して合算すると、合算後の分布は各グループのパラメータを合計したDirichlet分布に従います。
具体的には、物理ノード1に属するV個の成分(各パラメータ1)を合算すると、そのパラメータはVになります。同様に、物理ノード2、3、...Mについても同じです。
したがって、物理ノードの担当率ベクトル $(S_1, S_2, \dots, S_M)$ は次のようになります。
$$(S_1, S_2, \dots, S_M) \sim \mathrm{Dirichlet}(V, V, \dots, V)$$
に従います。
なぜこれが重要か
Dirichlet(V,V,...,V)分布の各物理ノードの担当率の期待値は、次のようになります。
$$\mathbb{E}[S_j] = \frac{V}{M \times V} = \frac{1}{M}$$
これは物理ノード数Mで均等に分散される理想的な値です。そして、Dirichlet分布のパラメータ $\alpha$(この場合はV)が大きいほど、各成分がこの期待値 $\frac{1}{M}$ の周りに集中します(分散が小さくなります)。つまり、仮想ノード数Vが大きいほど、物理ノード間の負荷偏りが小さくなります。これがVirtual Nodesによる負荷均等化のメカニズムです。
数理的な改善効果
M台の物理ノードが各V個の仮想ノードを持つとき、物理ノードの担当率の分散は次のようになります。
$$\mathrm{Var}(S_j) = \frac{V(MV - V)}{(MV)^{2}(MV+1)} = \frac{M-1}{M^{2}(MV+1)}$$
標準偏差は次のようになります。
$$\sigma = \sqrt{\frac{M-1}{M^{2}(MV+1)}}$$
この式は、Vが十分大きいときに $\sigma \approx \frac{1}{M\sqrt{V}}$ と近似できます。この近似式から、仮想ノード数Vに対して $1/\sqrt{V}$ で偏りを改善できることが分かります。
具体的には以下の通りです。
- 仮想ノード数を4倍にすると、偏りは半分になる
- 仮想ノード数を100倍にすると、偏りは1/10になる
Load Balancing Exporterでの実際の効果
Load Balancing ExporterはV=100を使っているので、実際の効果を計算してみましょう。
物理ノードM=3台の場合は次のようになります。
| 仮想ノード数V | 標準偏差σ | 評価 |
|---|---|---|
| 1(なし) | 23.6% | 仮想ノードなし |
| 100(実装値) | 2.7% | 実用的な小ささ |
V=1(仮想ノードなし)では標準偏差が23.6%もありますが、V=100にすると2.7%まで改善されます。約8.7倍の改善です。
これがLoad Balancing Exporterにおいて、デフォルトで100個の仮想ノードを使っている理由です。少数のWorkerでも、かなり均等な負荷分散が実現できています。
Virtual Nodesのトレードオフ
もちろん、Virtual Nodesにはトレードオフがあります。
メリット:
- 負荷偏りが減少する(標準偏差が $1/\sqrt{V}$ 倍)
- 少数の物理ノードでも均等な負荷分散が可能
デメリット:
- Ring上の点の数がM×Vに増えるため、メモリ使用量が増加する
ただし、M=3、V=100でも300エントリ程度なので、メモリ的には全く問題ありません。実用上は無視できるレベルです。
Worker数が少数のときの現実的な影響
ここまでの分析を踏まえて、僕が想定している2〜3台のWorker構成での実際の影響を整理してみます。
Virtual Nodeなしの場合(V=1)
| Worker数 | キー移動率(追加時) | 標準偏差 | 最大担当率 |
|---|---|---|---|
| 2→3 | 33.3% | 28.9% | 75.0% |
| 3→4 | 25.0% | 23.6% | 61.1% |
キー移動率が25〜33%、負荷偏りの標準偏差が23〜29%、最大担当率が平均の1.5〜1.8倍。これは無視できないレベルです。
Virtual Node=100の場合(Load Balancing Exporterの実装)
| Worker数 | キー移動率(追加時) | 標準偏差 | 評価 |
|---|---|---|---|
| 2→3 | 33.3%(不変) | 3.5% | 許容範囲 |
| 3→4 | 25.0%(不変) | 2.7% | 十分小さい |
Virtual Nodesは負荷偏りを改善しますが、キー移動率は変わりません。これは、ノード追加時にどれだけのキーが移動するかは、物理ノード数に依存するためです。
しかし、標準偏差が2.7〜3.5%まで改善されるので、負荷偏りは実用的なレベルに収まります。
結論
Worker数が2〜3台程度の構成では、以下のことが言えます。
- キー移動率は25〜33%程度発生するが、これはConsistent Hashingの特性上避けられません。
- Virtual Node=100により、負荷偏りは標準偏差2.7〜3.5%程度に抑えられます。
- スケールアウト時のキー移動は計画的に管理し、負荷偏りは監視で検知する運用が現実的です。
まとめ
- Consistent Hashingでは、$N$台から$(N+1)$台へのスケールアウト時に期待移動率は$\frac{1}{N+1}$となる
- $N=2 \rightarrow 3$で約33%、$N=3 \rightarrow 4$で25%のキーが移動する(ノード数が少ないと影響大)
- 各ノードの担当区間長は$\mathrm{Dirichlet}(1,1,\ldots,1)$分布に従い、これは「リング上でランダム配置したときの自然な偏り」を表現している
- Dirichlet分布の数学的性質から、標準偏差は$\sqrt{\frac{N-1}{N^{2}(N+1)}}$となり、最大担当率は調和数$H_N$を使って$\frac{H_{N}}{N}$と導出される
- Virtual Nodesを導入すると、負荷偏りの標準偏差は$\sqrt{\frac{M-1}{M^{2}(MV+1)}}$となり、$V$が大きいとき約$\frac{1}{M\sqrt{V}}$と近似され、仮想ノード数$V$に対して改善される
- Load Balancing Exporterは$V=100$を使っており、3台構成で標準偏差2.7%という実用的な偏りに抑えられる
- キー移動率は物理ノード数に依存するため、Virtual Nodesでは改善されない
Consistent Hashingの「ノード増減時の影響が小さい」という特性は、ノード数が多い場合に真価を発揮します。2〜3台みたいな少数ノードでは、キー移動率や負荷偏りが無視できないレベルになります。
ただし、Load Balancing ExporterがVirtual Nodesを使っていることで、負荷偏りは実用的なレベルに抑えられています。この数理的理解があれば、スケールアウト時に「約25%のキーが移動するけど、それは正常」と判断できますし、「負荷偏りは標準偏差2.7%程度に収まっているはず」という期待値を持てます。